Lösungen zur graphischen Nullstellenbestimmung
\(\\\)
Lösung 1
Die Funktion aufteilen in eine Gerade und eine Normalparabel:
\( \quad \begin{array}{ r c l l } 0 & = & x^2 - 2x - 3 & | + 2 x \\[5pt] 2x & = & x^2 - 3 & | + 3 \\[5pt] 2x + 3 & = & x^2 & \\[5pt] g(x) & = & h(x) & \\ \end{array} \)
\(\\\)
Mit dem Achsenabschnitt \(b=3\) und der Steigung \(m=2\)

\(\\\)
ergeben sich die Schnittstellen
\( \quad x_1=-1 \quad \textrm{und} \quad x_2=3 \; , \)
\(\\\)
die zugleich die Nullstellen von
\( \quad f(x) \, = \, x^2 - 2x - 3 \)
\(\\\)
und damit des Graphen \(f\) sind.

\(\\[2em]\)
Lösung 2
Die Funktion aufteilen in eine Gerade und eine Normalparabel:
\( \quad \begin{array}{ r c l l } 0 & = & x^2 - 3x + 2 & | + 3x \\[5pt] 3x & = & x^2 + 2 & | - 2 \\[5pt] 3x - 2 & = & x^2 & \\[5pt] g(x) & = & h(x) & \\ \end{array} \)
\(\\\)
Mit dem Achsenabschnitt \(b=-2\) und der Steigung \(m=3\)

\(\\\)
ergeben sich die Schnittstellen
\( \quad x_1=1 \quad \textrm{und} \quad x_2=2 \; , \)
\(\\\)
die zugleich die Nullstellen von
\( \quad f(x) \, = \, x^2 - 3x + 2 \)
\(\\\)
und damit des Graphen \(f\) sind.

\(\\[2em]\)
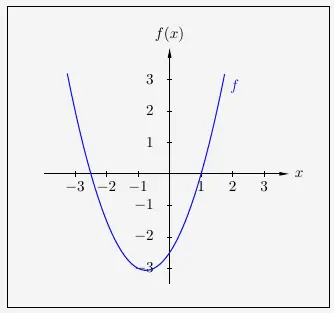
Lösung 3
Die Funktion aufteilen in eine Gerade und eine Normalparabel:
\( \quad \begin{array}{ r c l l } 0 & = & x^2 + \frac{3}{2} x - 2{,}5 & | - \frac{3}{2} x \\[5pt] -\frac{3}{2} x & = & x^2 - 2{,}5 & | + 2{,}5 \\[5pt] -\frac{3}{2} x + 2{,}5 & = & x^2 & \\[5pt] g(x) & = & h(x) & \\ \end{array} \)
\(\\\)
Mit dem Achsenabschnitt \(b=2{,}5\) und der Steigung \(m=- \frac{3}{2}\)

\(\\\)
ergeben sich die Schnittstellen
\( \quad x_1=-2{,}5 \quad \textrm{und} \quad x_2=1 \; , \)
\(\\\)
die zugleich die Nullstellen von
\( \quad f(x) \, = \, x^2 + \frac{3}{2} x - 2{,}5 \)
\(\\\)
und damit des Graphen \(f\) sind.
\(\\[1em]\)